So, well, after a lot of re-edits and excerpting, and changes, the joint article of Debdyuti and mine on Neuberg Locus has found its place in the Second Volume of the Journal of Classical Geometry. I had to change and redraw all the diagrams in metapost, and now I feel that all the tedious work was worth it. 🙂
I’m personally thankful to A.V.Akopyan for helping out with the and metapost issues of the article. The full article, as appeared in the Volume 2, is uploaded here.
And well, a small update on my current status… I am currently burdened with Board Exams and stuff (Chemistry exam tomorrow), and all these Exams Business will end on 2nd June. Before that, I’m sorry that I can’t update the blog at all. 😦

And you were saying me today , that are not that good in geometry 😀 ! ! !
Wonderous ! , I beleive that there are very less indians of age group 16-18 who have got there article in a international journal …
Now you can say , INMO hardly matters , your passion toward mathematics matter 😀
Hello, i was reading your solution and found next result: and a point
and a point 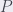 , suppose,
, suppose,  ,
, 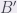 ,
,  are reflections of point
are reflections of point 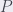 wrt sides of
wrt sides of  ,
,  ,
,  ,
, 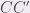 intersects at point
intersects at point  ,
,  is isogonal to
is isogonal to  , then we can prove that circumcenter of
, then we can prove that circumcenter of  is on line
is on line  . I saw figure 5 from your proof and found another nice solution of Neuberg problem.
. I saw figure 5 from your proof and found another nice solution of Neuberg problem.
Problem
Given a triangle
I think we proved this property in the article. 🙂
If possible, can you give us some ideas on your proof? 🙂
This problem is equivalent to next:
Given a triangle ABC and a point P, suppose, A’,B’,C’ are reflections of point P wrt sides of ABC,AA’, BB’, CC’ intersects at point Q, Q’ is second intersection point of circles AA’P, BB’P, CC’P then we can prove that circumcenter of ABC is on line PQ’.
I’m pretty sure the answer to this entire thing is “curry.” The principle of stinx developed by observing certain sm types proves beyond a shadow of a doubt that curry not only solves, but also answers, the mysteries of the universe.
hi
i will necropost
asdfasdfasdf
asdfasdfasdf
where is potla